Program & algorithm for Quick sort in C

When we are working on for sorting data,  we often look at its worst-case running time and in that case, quicksort is the fastest known sorting algorithm, it is often the best practical choice for sorting, as its average expected running time is O(n log(n)). 

Quick sort algorithm is a highly efficient sorting algorithm and is based on divide and conquer strategy. In a quick sort we take the one element called as a pivot, then we list all the smaller elements than a pivot, and greater than a pivot. after partitioning we have the pivot in the final position. After recursively sorting the partition array, we get the sorted elements.

This algorithm divides the list into three main parts:

1. Elements less than the Pivot element
2. Pivot element(Central element)
3. Elements greater than the pivot element

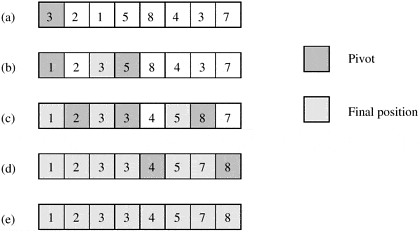
Algorithm for quick sort can be explained as below, the divide-and-conquer strategy is used in quicksort. Below is the recursion step as described:

1. Choose a pivot value. We take the value of the middle element as pivot value, but it can be any value, which is in range of sorted values, even if it doesn't present in the array.
2. Reorder the list so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
3. Recursively sort the sub-list of lesser elements and the sub-list of greater elements.

The complexity of the quicksort algorithm in the worst case is O(n²), in both best and average cases are O(n log n) where n is the number of unsorted elements.

Image Source: Wikipedia

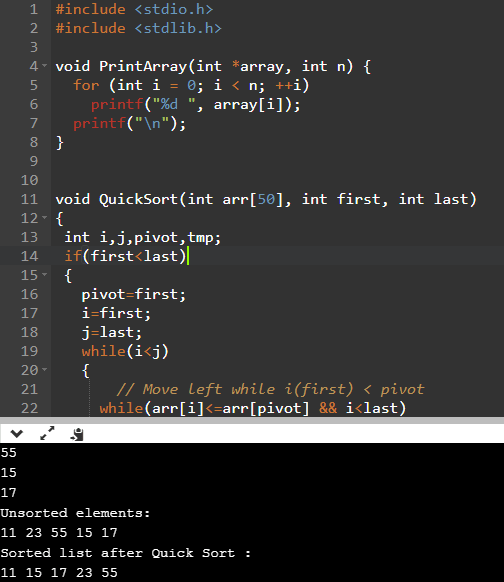
Quick sort program in C

#include <stdio.h>

//printing array list code 
void PrintArray(int *array, int n) {
  for (int i = 0; i < n; ++i)
    printf("%d ", array[i]);
  printf("\n");
}
 
//main quick sort logic function 
void QuickSort(int arr[50], int first, int last)
{
 int i,j,pivot,tmp;

 if(first<last)
 {
   //get pivot element as first
   pivot=first;
   i=first;
   j=last;
   while(i<j)
   {
       // Move left while i(first) < pivot 
     while(arr[i]<=arr[pivot] && i<last)
        i++;
        // Move right while j(last) > pivot 
     while(arr[j]>arr[pivot])
        j--;
        
     if(i<j)
     {
        tmp=arr[i];
        arr[i]=arr[j];
        arr[j]=tmp; 
     }
   }
   tmp=arr[pivot];
   arr[pivot]=arr[j];
   arr[j]=tmp;
   
   QuickSort(arr,first,j-1);
   QuickSort(arr,j+1,last);
 }
}
 
void main() {

     int array[50], i, n;
     printf("Enter no. of elements: \n"); 
     scanf("%d", &n);
     printf("Enter the elements: \n");
     for (i=0; i<n; i++)
     {
      scanf ("%d", &array[i]);
     }
     
     printf("Unsorted elements: \n");
     PrintArray(array, n);
     
     QuickSort(array, 0,n-1);
     
     printf("Sorted list after Quick Sort :\n");
     PrintArray(array, n);
     
}

Output

Enter no. of elements: 
5
Enter the elements: 
11
23
55
15
17
Unsorted elements: 
11 23 55 15 17 
Sorted list after Quick Sort :
11 15 17 23 55 

You can check the working example online https://onlinegdb.com/SkOigLOgm

How does it work?

On the partition, step program divides the array into two parts and every element i from the left part is less or equal than every element j from the right part. Also i and j satisfy i = pivot = j inequality. After completion of the recursion calls both of the parts become sorted and, taking into account arguments stated above, the whole array is sorted.

You may also like:

Program for insertion sorting in C (With explanation)

Stack Program in C (Concept, Algorithm & C program example)

If you have any question's regarding this article, feel free to ask your question's in comment's below.