In the previous article, we mentioned about fibonacci series in C, now in this article, we have mentioned C Program to print Fibonacci Triangle.
Fibonacci series:
The Fibonacci series was discovered by the Italian mathematician named Leonardo Fibonacci. Fibonacci numbers are denoted as Fn. Fibonacci has so many examples in our real life, biology, human organs, music, art, pascals’ triangle, stock market, coding, trading, mathematics, the Fibonacci numbers are useful for programming algorithms.
These are the positive numbers in the sequence by adding the two foregoing numbers. All the numbers are the sum of previous numbers in the sequence like 0,1,1,2,3,5,8,13,21,34,55,89....these are known as Fibonacci numbers. The sequence starts from 0 and 1 which is direct. Fibonacci numbers are also defined as a recurrence relation.
How to calculate Fibonacci Numbers?
So here, we will learn about the Fibonacci series. Fibonacci numbers are obtained by adding the sum of the last two numbers together. The sequence looks like 0,1,1,2,3,5,8,13,21 and goes on by adding previous two numbers.
- By adding these two numbers we get (0+1)=1,
- By taking the last two numbers we get (1+1)=2,
- Add the previous two numbers we get (1+2)=3,
- Add the previous two numbers we get (2+3)=5,
And it goes on...
The formula to get Fibonacci series: Fn = Fn-1 + Fn-2
here, Fn is the number
- (n-1)th is Fn-1
- (n-2)th is Fn-2
In this table, all the numbers are given, have a look
- The first term is 0
- The second term is 1
- The third term is 1
- The Fourth term is 2
- The fifth term is 3
- The sixth term is 5
- The seventh term is 8
- The eighth term is 13
- The ninth term is 21
- The tenth term is 34
Applications of Fibonacci Numbers:
We can find all the applications in our daily lives like plants, fruits, animals, human beings, mathematics, coding, and many more.
some of the applications are as follows:
- It can be seen in pascal’s triangle and Pythagorean triples.
- In converting kilometers to miles
- The golden ratio used for designing websites and structures
- A betting system as it requires a mathematical Fibonacci sequence
- For computer systems like coding, run time analysis of Euclid’s algorithm as it’s used to get the greatest common divisor of two numbers.
- We can also see them in our surroundings like human heads, bodies, music, snail shells, spider webs, plants(which is also known as phyllotaxis), flower petals, etc.
Fibonacci program in C
Now we will learn how to code the Fibonacci series 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 ....so here below is my code to find out the Fibonacci series.
#include <stdio.h>
int main() {
int i, n ;
int first = 0, second = 1;
int sum = first + second ;
printf("Enter the number of terms for the Fibonacci series: ");
scanf("%d", &n);
printf("Fibonacci Series: %d, %d, ", first, second);
for (i = 3; i <= n; ++i) {
printf("%d, ", sum);
first = second ;
second = sum;
sum = first + second;
}
return 0;
}Output:
Enter the number of terms for the Fibonacci series: 10
Fibonacci Series: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34..Explanation:
Let’s suppose n=10, we need to print n numbers of the Fibonacci series. We have taken the first two elements first and second, which we will add together to get the next term.
we need to repeat the loop as many times as we need to print the series. we need to add the values of the first and second term and store them sum= first+second.
we will store the second value in the first and the sum value in the second. this is how you will get the series 0, 1, 1, 2, 3, 5, 8, 13, 21, 34
Program to print Fibonnaci pyramid triangle in C
The Fibonacci triangle is also known as Hosoya’s Triangle. In this triangle, all the numbers are the Fibonacci numbers in the sequence which is the sum of two preceding numbers.
Now we will learn to code for the Fibonacci Triangle.
#include <stdio.h>
#include<stdlib.h>
int main()
{
int i,j,k,c;
int a= 0, b=1;
for(i=1; i<=5; i++)
{
printf("%d\t",b);
for(k=1; k<i; k++)
{
c=a+b;
printf("%d\t",c);
a=b;
b=c;
}
printf("\n");
}
}Output:
1
1 1
1 2 3
3 5 8 13
13 21 34 55 89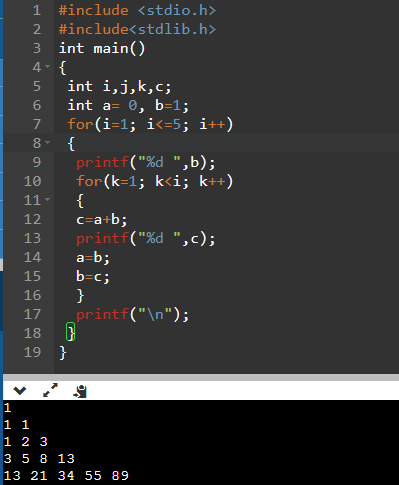
Explanation:
In this code, we have used a two-loop one for the series and another for the row.
We did the same process to get the Fibonacci series in the first loop by adding the last two numbers while storing values.
In the second loop, we will shift those values in a row to get the triangle.
You may also like
Program for Matrix multiplication in C (With & Without pointers)
