Selection sort program in C (With Algorithm)

: 7047

Last Updated : 15/06/2018

Posted By :- Vinnu

Selection sort is a sorting algorithm that has a quadratic running time complexity of O(n2 ), thereby making it inefficient to be used on large lists.

Although selection sort performs worse than insertion sort algorithm, it is noted for its simplicity and also has performance advantages over more complicated algorithms in certain situations. Selection sort is generally used for sorting files with very large objects (records) and small keys.

In comparison with other quadratic sorting algorithms it almost always outperforms bubble sort, but it is usually slower than insertion sort.

The idea of selection sort is, that if we sort the array from largest to smallest element, than the first element of the sorted array will be the one with the largest value. Second will be the largest element of the rest of the array. Third will be the largest element of the new rest of the array (initial array without the two already sorted elements)...

So we can iteratively select the largest element of the (reduced) array, swap it with the first element and than reduce the problem size by 1 (sort only the rest of the array). When there remains only one element to sort, the algorithm terminates.

Consider an array ARR with N elements. Selection sort works as follows:

First find the smallest value in the array and place it in the first position. Then, find the second smallest value in the array and place it in the second position. Repeat this procedure until the entire array is sorted. Therefore,

In Pass 1, find the position POS of the smallest value in the array and then swap ARR[POS] and ARR[0]. Thus, ARR[0] is sorted.
In Pass 2, find the position POS of the smallest value in sub-array of N–1 elements. Swap ARR[POS] with ARR[1]. Now, ARR[0] and ARR[1] is sorted.
In Pass N–1, find the position POS of the smaller of the elements ARR[N–2] and ARR[N–1]. Swap ARR[POS] and ARR[N–2] so that ARR[0], ARR[1], ..., ARR[N–1] is sorted.

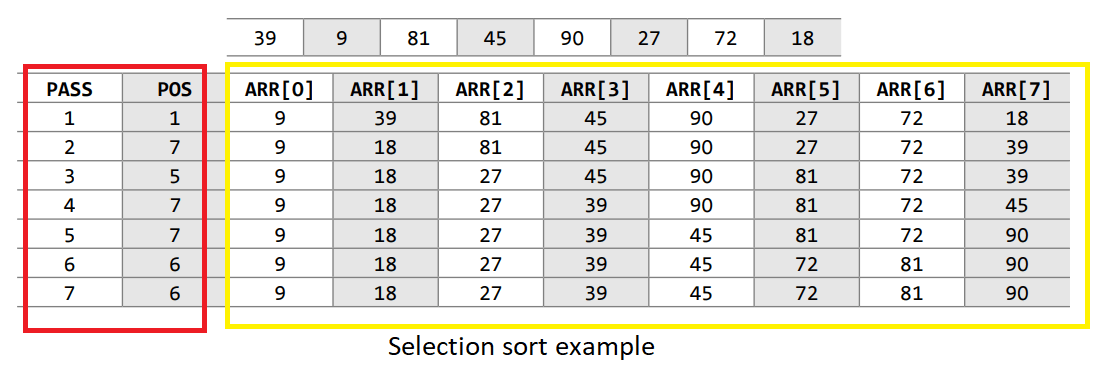
The above image shows position of the smallest element to compare in each pass, you will see at each pass one element get sorted, like in pass 1, 1st position element is sorted in pass 2, 2nd element is sorted and so on.

Selection sort algorithm

// SMALLEST (ARR, K, N, POS) , function name

Step 1:[INITIALIZE] SET SMALL = ARR[K]
Step 2:[INITIALIZE] SET POS=K
Step 3:Repeat forJ= K+1 to N
         IF SMALL > ARR[J]
         SET SMALL = ARR[J]
         SET POS=J
       [END OF IF]
       [END OF LOOP]
Step 4: RETURN POS


// Another function, SELECTION SORT(ARR, N)
Step 1: Repeat Steps 2 and 3 for K=1 to N-1
Step 2: CALL SMALLEST(ARR, K, N, POS)
Step 3: SWAP A[K] with ARR[POS]
        [END OF LOOP]
Step 4: EXIT

In the above algorithm, we have divided the sorting into two functions.

In the algorithm, during the Kth pass, we need to find the position POS of the smallest elements from ARR[K], ARR[K+1], ..., ARR[N]. To find the smallest element, we use a variable SMALL to hold the smallest value in the sub-array ranging from ARR[K] to ARR[N]. Then, swap ARR[K] with ARR[POS]. This procedure is repeated until all the elements in the array are sorted.

Selection sort program in C

#include <stdio.h>
#include <stdlib.h> 
#include <conio.h>
 
int smallest(int arr[], int k, int n);
void selection_sort(int arr[], int n);
  
void main() {
  int arr[10], i, n;
  printf("\n Enter the number of elements in the array: ");
  scanf("%d", &n);
  printf("\n Enter the elements of the array: ");
  for (i = 0; i < n; i++) {
    scanf("%d", &arr[i]);
  }
  selection_sort(arr, n);
  
  printf("\n The sorted array is: \n");
  for (i = 0; i < n; i++)
  {
    printf(" %d\t", arr[i]);
  }
}

//get smallest element from the array 
int smallest(int arr[], int k, int n) {
  int pos = k, small = arr[k], i;
  
  for (i = k + 1; i < n; i++) {
    if (arr[i] < small) {
      small = arr[i];
      pos = i;
    }
  }
  return pos;
}

//find smallest element position calling above function
//swap it with the current pass/position of array
void selection_sort(int arr[], int n) {
  int k, pos, temp;
  for (k = 0; k < n; k++) {
    pos = smallest(arr, k, n);
    temp = arr[k];
    arr[k] = arr[pos];
    arr[pos] = temp;
  }
}

Output of the above code when executing online here

 Enter the number of elements in the array: 5

 Enter the elements of the array: 22 5 678 102 33

 The sorted array is: 
 5	 22	 33	 102	 678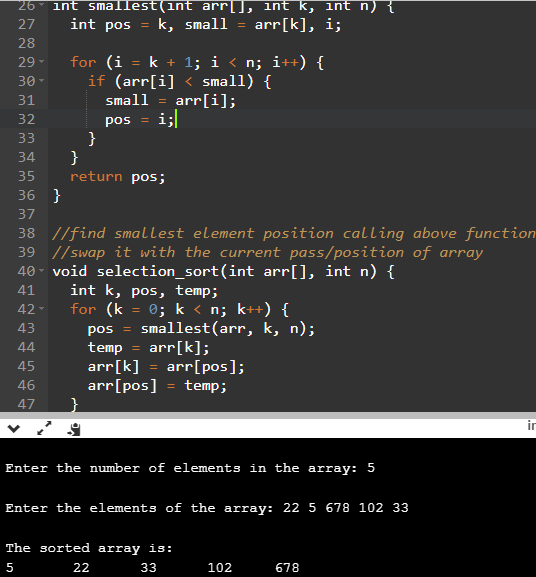

You maye also like to view:

Merge sort algorithm in C with Program sample

Bubble sort algorithm in C (With sample program)

Program & algorithm for Quick sort in C