Infix, postfix, and prefix notations are three different but equivalent notations of writing algebraic expressions. But before learning about prefix and postfix notations, let us first see what an infix notation is. We all are familiar with the infix notation of writing algebraic expressions.
While writing an arithmetic expression using infix notation, the operator is placed in between the operands. For example, A+B; here, plus operator is placed between the two operands A and B.
Although it is easy for us to write expressions using infix notation, computers find it difficult to parse as the computer needs a lot of information to evaluate the expression. Information is needed about operator precedence and associativity rules, and brackets which override these rules. So, computers work more efficiently with expressions written using prefix and postfix notations.
In postfix notation, as the name suggests, the operator is placed after the operands. For example, if an expression is written as A+B in infix notation, the same expression can be written as AB+ in postfix notation. The order of evaluation of a postfix expression is always from left to right. Even brackets cannot alter the order of evaluation.
The expression (A + B) * C can be written as: [AB+]*C => AB+C* in the postfix notation
Conversion of an Infix Expression into a Postfix Expression
Let I be an algebraic expression written in infix notation. I may contain parentheses, operands, and operators. For simplicity of the algorithm we will use only +, –, *, /, % operators.
The precedence of these operators can be given as follows:
Higher priority *, /, %
Lower priority +, –No doubt, the order of evaluation of these operators can be changed by making use of parentheses.
For example, if we have an expression A + B * C, then first B * C will be done and the result will be added to A. But the same expression if written as, (A + B) * C, will evaluate A + B first and then the result will be multiplied with C
Algorithm to transform an infix expression into the postfix expression
Step 1: Add ")" to the end of the infix expression
Step 2: Push "(" on to the stack
Step 3: Repeat until each character in the infix notation is scanned
IF a "(" is encountered, push it on the stack
IF an operand (whether a digit or a character) is encountered, add it
postfix expression.
IF a ")" is encountered, then
a. Repeatedly pop from stack and add it to the postfix expression until a ( is
encountered.
b. Discard the "(" . That is, remove the "(" from stack and do not
add it to the postfix expression
IF an operator is encountered, then
a. Repeatedly pop from stack and add each operator (popped from the stack) to
the postfix expression which has the same precedence or a higher precedence
than 0
b. Push the operator to the stack
[END OF IF]
Step 4: Repeatedly pop from the stack and add it to the postfix expression until the
stack is empty
Step 5: EXITThe algorithm accepts an infix expression that may contain operators, operands, and parentheses. For simplicity, we assume that the infix operation contains only modulus (%), multiplication (*), division (/), addition (+), and subtraction (?) operators and that operators with the same precedence are performed from left-to-right.
The algorithm uses a stack to temporarily hold operators. The postfix expression is obtained from left-to-right using the operands from the infix expression and the operators which are removed from the stack.
The first step in this algorithm is to push a left parenthesis on the stack and to add a corresponding right parenthesis at the end of the infix expression. The algorithm is repeated until the stack is empty.
C program to convert infix to postfix using stack
#include <stdio.h>
#include <ctype.h>
#define SIZE 50
char stack[SIZE];
int top=-1; /* Global declarations */
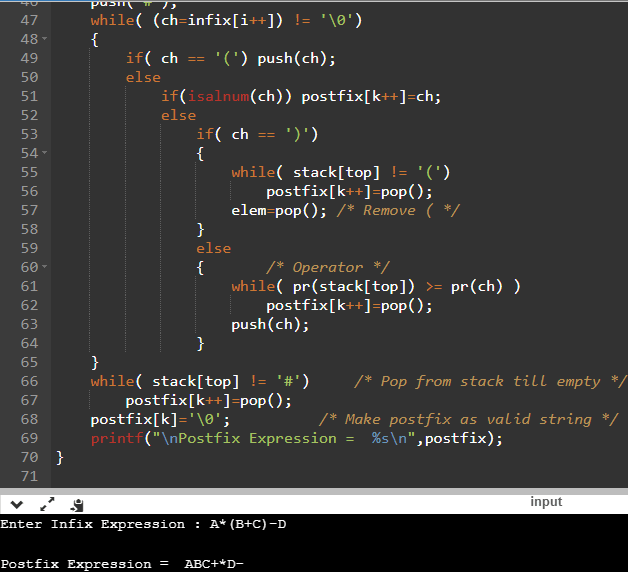
push(char elem)
{ /* Function for PUSH operation */
stack[++top]=elem;
}
char pop()
{ /* Function for POP operation */
return(stack[top--]);
}
int pr(char symbol)
{ /* Function for precedence */
if(symbol == '^')/* exponent operator, highest precedence*/
{
return(3);
}
else if(symbol == '*' || symbol == '/')
{
return(2);
}
else if(symbol == '+' || symbol == '-') /* lowest precedence */
{
return(1);
}
else
{
return(0);
}
}
/* Main Program */
void main()
{
char infix[50],postfix[50],ch,elem;
int i=0,k=0;
printf("Enter Infix Expression : ");
scanf("%s",infix);
push('#');
while( (ch=infix[i++]) != '\0')
{
if( ch == '(') push(ch);
else
if(isalnum(ch)) postfix[k++]=ch;
else
if( ch == ')')
{
while( stack[top] != '(')
postfix[k++]=pop();
elem=pop(); /* Remove ( */
}
else
{ /* Operator */
while( pr(stack[top]) >= pr(ch) )
postfix[k++]=pop();
push(ch);
}
}
while( stack[top] != '#') /* Pop from stack till empty */
postfix[k++]=pop();
postfix[k]='\0'; /* Make postfix as valid string */
printf("\nPostfix Expression = %s\n",postfix);
}
Afer executing the above code here https://onlinegdb.com/Hy6rsGOZX got the output as below
Enter Infix Expression : A*(B+C)-D
Postfix Expression = ABC+*D-
You may also like:
